Solving Exponential Equations Worksheet with Answers PDF: A Comprehensive Guide
Exponential equations worksheets, often in PDF format, provide targeted practice for students mastering these crucial algebraic skills. These resources frequently include answer keys,
facilitating self-assessment and efficient learning.
Understanding Exponential Equations
Exponential equations are mathematical statements where a variable appears in an exponent; These equations differ significantly from linear or quadratic equations, demanding a unique approach to solving. A core concept involves recognizing the fundamental structure: a base raised to a variable exponent.

Worksheets dedicated to these equations often begin by reinforcing this understanding, asking students to identify exponential functions and distinguish them from other function types. The focus extends to grasping how changes in the exponent dramatically affect the outcome, unlike linear relationships.
Successfully tackling these problems requires familiarity with the properties of exponents—product of powers, quotient of powers, power of a power—and a solid grasp of logarithmic functions. PDF worksheets with answers are invaluable tools for practice, allowing students to check their work and solidify their comprehension of these essential mathematical principles.
What are Exponential Functions?
Exponential functions represent growth or decay at a rate proportional to the current value. They take the general form f(x) = ax, where ‘a’ is a constant base and ‘x’ is the variable in the exponent. Unlike linear functions with a constant rate of change, exponential functions exhibit a rapidly accelerating or decelerating rate.
Worksheets focusing on these functions often present scenarios involving compound interest, population growth, or radioactive decay – real-world applications demonstrating their power. Identifying these functions from a set of equations is a common exercise, preparing students for solving more complex problems.
PDF resources with answer keys are crucial for self-paced learning. They allow students to verify if they correctly recognize the characteristics of an exponential function and differentiate it from other types. Mastering this identification is the first step towards confidently solving exponential equations.
The Basic Form of an Exponential Equation
The fundamental structure of an exponential equation involves a variable within the exponent. A typical form is abx + c = d, where ‘a’ is the base, ‘b’ and ‘c’ are constants, ‘x’ is the unknown variable, and ‘d’ is a constant value. Worksheets frequently present variations of this form, testing a student’s ability to isolate the exponential term.
Solving these equations often requires employing logarithmic properties or utilizing the one-to-one property when bases are equal. PDF practice materials with detailed answer keys are invaluable for understanding each step of the solution process. Recognizing this basic form is essential for applying the correct solving techniques.
Many worksheets begin with simpler equations, gradually increasing complexity to build proficiency. These resources aim to solidify understanding of how to manipulate exponential expressions and isolate the variable ‘x’.
Key Properties of Exponential Functions
Understanding the inherent properties of exponential functions is crucial when tackling worksheets designed to test problem-solving skills. A core property is that exponential growth (when the base is greater than 1) results in a rapidly increasing function, while exponential decay (base between 0 and 1) leads to a decreasing function.
Another vital property is the one-to-one nature of exponential functions; if am = an, then m = n. This principle is frequently utilized in solving equations. PDF resources with answer keys often highlight these properties, providing examples of their application.
Furthermore, recognizing the impact of the exponent on the function’s behavior is key. Worksheets often assess this understanding through various problem types, reinforcing the connection between the function’s form and its graphical representation.

Methods for Solving Exponential Equations
Worksheets commonly focus on two primary methods: utilizing the one-to-one property and employing logarithms. Answer keys verify correct application of these techniques.
Using the One-to-One Property
The one-to-one property is a powerful tool when solving exponential equations, particularly those where both sides of the equation can be expressed with the same base. Worksheets often present problems designed to test this skill, requiring students to manipulate exponential expressions to achieve a common base.
If ax = ay, then x = y. This fundamental principle allows for direct comparison of exponents once the bases are equalized. For example, if a worksheet presents 2x = 8, students must recognize that 8 is equivalent to 23, leading to the solution x = 3.
Exponential equations worksheet with answers PDF resources frequently include examples where students must first rewrite terms to share a common base before applying the one-to-one property. The answer key provides verification of these steps, ensuring a solid understanding of this method. Mastering this property simplifies solving many exponential equations without resorting to logarithms.
Taking the Logarithm of Both Sides
When exponential equations don’t readily lend themselves to the one-to-one property – meaning bases aren’t easily equalized – taking the logarithm of both sides becomes essential. Worksheets dedicated to solving these equations emphasize this technique, often requiring students to choose an appropriate logarithmic base (common or natural).
Applying a logarithm to both sides doesn’t change the equation’s validity but allows you to “bring down” the exponent as a coefficient. For instance, solving 5x = 13 involves taking the log base 10 (or ln) of both sides: log(5x) = log(13), which simplifies to x*log(5) = log(13).
Exponential equations worksheet with answers PDF materials provide step-by-step examples and answer keys to guide students through this process. These resources demonstrate how to isolate ‘x’ by dividing both sides by log(5). Understanding this method is crucial for tackling more complex exponential problems.
When to Use Logarithms: A Decision Guide
Determining when to employ logarithms for solving exponential equations is a key skill reinforced in worksheets. If the equation can be rewritten so both sides have the same base, the one-to-one property is the simpler route. However, when bases differ, logarithms become necessary.
A helpful guide: if a variable appears in the exponent and you can’t manipulate the equation to achieve common bases, logarithms are your go-to method. Exponential equations worksheet with answers PDF resources often present scenarios illustrating this decision process.
Consider 2x = 3 versus 2x+1 = 6. The first requires a logarithm, while the second can be rewritten as 2x * 2 = 6, then 2x = 3, necessitating a logarithm. Mastering this discernment, aided by detailed answer keys, is vital for efficient problem-solving.

Types of Exponential Equations & Solving Techniques
Exponential equations worksheets present diverse problems, from those with identical bases to those demanding logarithmic solutions, alongside variable exponents.
Equations with the Same Base

When exponential equations share a common base, solving them becomes remarkably straightforward. Worksheets focusing on this type emphasize utilizing the fundamental property: if ax = ay, then x = y. This principle allows direct equating of exponents, bypassing the need for logarithms.
For instance, consider an equation like 23x+1 = 25x-3. Applying the property, we immediately deduce 3x + 1 = 5x ー 3. Solving this linear equation yields x = 2. Exponential equations worksheet problems often start with these simpler scenarios to build confidence.
Answer keys accompanying these worksheets demonstrate this process step-by-step. Students practice identifying the common base and correctly applying the exponent-equating rule. Mastery of this technique is crucial, as it forms the foundation for tackling more complex exponential equations. Kuta Software often includes these types of problems in their practice sets.
Equations with Different Bases – Using Logarithms
When exponential equations present differing bases, the direct exponent-equating method fails. This is where logarithms become indispensable. Worksheets dedicated to this scenario guide students through applying logarithmic properties to isolate the variable. The core strategy involves taking the logarithm of both sides of the equation – using either the common (base-10) or natural (base-e) logarithm.
For example, solving 32x = 5x+1 requires applying a logarithm. Taking the log of both sides yields log(32x) = log(5x+1). Utilizing the power rule of logarithms (log(ab) = blog(a)), we get 2xlog(3) = (x+1)*log(5).
Expanding and rearranging, students solve for x. Answer keys provide detailed solutions, showcasing each logarithmic step. These worksheets emphasize careful application of logarithmic rules and accurate calculations. Resources like Kuta Software offer extensive practice in this area, building proficiency in handling complex exponential equations.
Equations Involving Exponential Functions with Variables in the Exponent
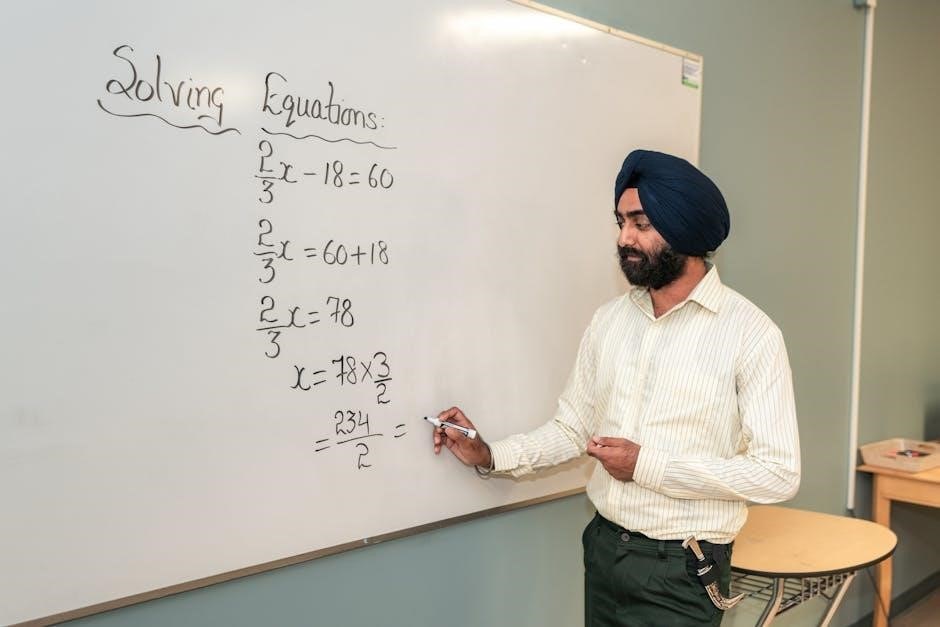
Worksheets focusing on exponential equations where the variable resides within the exponent demand a strong grasp of logarithmic principles. These problems, like 2x+3 = 7, cannot be solved through simple algebraic manipulation. The key lies in utilizing logarithms to “bring down” the variable from the exponent.
Students learn to apply the logarithm to both sides: log(2x+3) = log(7). Then, employing the power rule of logarithms – log(ab) = blog(a) – transforms the equation into (x+3)log(2) = log(7). Isolating ‘x’ involves dividing both sides by log(2) and subtracting 3, resulting in x = (log(7)/log(2)) ー 3.
Answer keys accompanying these worksheets demonstrate this process step-by-step. Practice with resources like Kuta Software reinforces this technique. Mastering these equations is crucial, as they frequently appear in advanced mathematical contexts and real-world applications.

Worksheet Practice & Resources
Numerous exponential equations worksheets with answers are readily available online, including options from Kuta Software, offering diverse practice problems and skill reinforcement.
Common Types of Problems on Exponential Equation Worksheets
Exponential equation worksheets commonly present a variety of problem types designed to build proficiency. Students frequently encounter problems requiring them to solve for an unknown variable within the exponent, often involving simplifying expressions like 22x+3. Another prevalent type focuses on identifying exponential functions from given equations or graphs.
Worksheets also include equations with the same base, allowing students to apply the one-to-one property. More challenging problems necessitate using logarithms to solve equations with different bases, such as 3x = 5. Furthermore, students practice converting between exponential and logarithmic forms.
Many worksheets incorporate real-world application problems, like compound interest or population growth, requiring students to model scenarios with exponential functions. Finally, a significant portion focuses on verifying solutions to ensure accuracy, emphasizing the importance of checking answers within the original equation. Answer keys are crucial for self-assessment.
Finding Exponential Equations Worksheet with Answers PDF Online
Numerous online resources offer exponential equations worksheets in PDF format, often accompanied by answer keys. Websites like Kuta Software provide a vast library of free, printable worksheets covering various difficulty levels. A simple web search using keywords like “exponential equations worksheet PDF” yields numerous results from educational websites and teacher resource platforms.
Many platforms categorize worksheets by topic and skill level, allowing targeted practice. Websites offering interactive worksheets with immediate feedback are also available. When downloading PDFs, ensure the source is reputable to guarantee accuracy of both the problems and the answer key.
Educational blogs and online tutoring services frequently provide free downloadable worksheets as supplementary materials. Always preview the worksheet to confirm it aligns with the specific concepts being studied. Utilizing these online resources streamlines access to practice materials and facilitates efficient learning.
Utilizing Kuta Software for Practice
Kuta Software is a widely recognized provider of mathematics worksheets, including extensive resources for practicing exponential equations. Their offerings encompass a range of difficulty levels, from basic identification to complex problem-solving, all available in convenient PDF format with comprehensive answer keys.
Kuta Software’s worksheets often focus on specific skills, such as solving equations requiring logarithms or those with the same base. The software allows for customization, enabling educators to generate worksheets tailored to their students’ needs. These worksheets are particularly valuable for reinforcing concepts and building fluency.

Access to Kuta Software resources typically requires a subscription, but the investment provides access to a vast library of high-quality materials. The clear formatting and detailed answer keys make self-assessment and independent practice highly effective. It’s a powerful tool for mastering exponential equations.

Answer Key & Checking Solutions
Answer keys accompanying exponential equations worksheets are vital for verifying solutions. Always substitute your answer back into the original equation to confirm accuracy.
Importance of Verifying Solutions
Verifying solutions is a non-negotiable step when working with exponential equations worksheets. While applying logarithmic properties or utilizing the one-to-one property might lead to a potential solution, it doesn’t guarantee its correctness. Exponential functions can sometimes introduce extraneous solutions – values that satisfy the manipulated equation but not the original one.
Substituting your obtained answer back into the initial exponential equation allows you to rigorously test its validity. This process reveals whether the solution truly satisfies the original relationship between the variables and the exponent. Failing to verify can lead to incorrect conclusions and propagate errors in subsequent calculations.
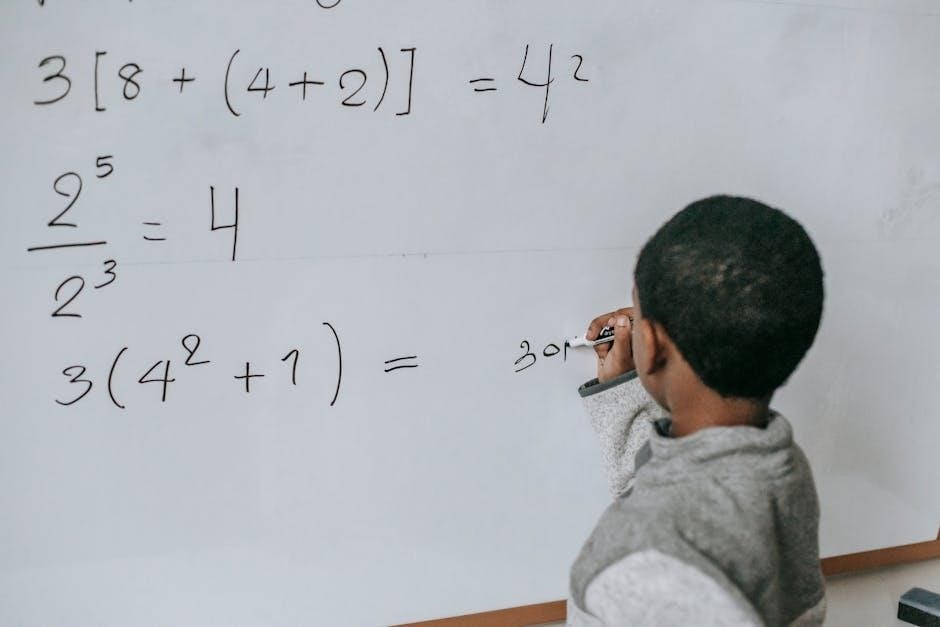
Worksheets with answer keys are excellent tools for self-checking, but understanding why verification is crucial is paramount. It reinforces a deeper comprehension of exponential functions and the potential pitfalls in solving equations. A correct solution will always satisfy the original equation, providing confidence in your mathematical work.
Common Errors to Avoid When Solving
When tackling exponential equations worksheets, several common errors can derail your progress. A frequent mistake involves incorrectly applying the rules of exponents – misremembering power-of-a-power or product-of-powers rules. Another pitfall is failing to properly isolate the exponential term before applying logarithms, leading to inaccurate results.
Students often struggle with the correct application of logarithmic properties, particularly when dealing with different bases. Remember to utilize the change-of-base formula when necessary. Forgetting to verify your answer, as discussed previously, is a significant oversight. Always substitute back into the original equation!
Carelessly handling negative signs or overlooking the possibility of extraneous solutions are also common. Utilizing answer keys to check your work is helpful, but focus on understanding where you went wrong, not just obtaining the correct answer. Practice and careful attention to detail are key to mastering these concepts.
Where to Find Reliable Answer Keys
Locating trustworthy answer keys for exponential equations worksheets is crucial for effective self-study. Kuta Software, a popular resource, frequently provides answer keys alongside its worksheets, ensuring accuracy and alignment with the problems. Many educational websites specializing in mathematics offer free worksheets with corresponding answer keys, though verifying their source is advisable.
Teachers and professors often share answer keys through learning management systems or directly with students. Online forums dedicated to mathematics can also be valuable, but exercise caution and cross-reference solutions. Websites offering step-by-step solutions, like those focusing on algebra, can supplement answer keys by explaining the process.
Always prioritize answer keys from reputable sources to avoid reinforcing incorrect methods. Remember, the goal isn’t just to get the right answer, but to understand the underlying principles of solving exponential equations.